Computation and Improvisation
Computation and Improvisation
Scott Snibbe
ICC Journal, Tokyo Japan, Fall, 2002
Media can be broadly broken down into those that are static—constructed once, and then perceived as long as the artifact remains—and those that are actively reconstructed. Media such as painting and sculpture fall into the former category, while music and performance fall into the latter. Two forms of music present radically different approaches to reproduction. In notational musical systems, the work is translated from symbolic form (notes or memories) into the manipulations of an instrument. In musical systems such as Indian ragas, Balinese gamelan and jazz, a work is expressed as a set of rules for interacting melodically and rhythmically with the other performers. By its reproduction through a set of rules rather than a precise description, improvisational music can be considered computational – the translation of a set of abstract codes into a physical expression through a defined set of rules.
Examples of static and dynamic creation can also be seen in computer-based art. The computer can serve as a reliable tool with which to create a static artifact--such as a two- dimensional print or a stereolithographic sculpture. Artists working in the realm of interactivity, including myself, use computers in the role of the raga player or jazz musician – a dynamic participant in a rule-based game that produces meaning for the viewers.
In many ways, conceptual art is the logical precursor to computer-based installation art, since in conceptual art the medium of expression first becomes elusive. The father of conceptual art, Marcel DuChamp, provides some of the clearest examples of both static and dynamic expression in conceptual art. Works such as Fountain (1917) present a static artifact—in this case, a signed urinal. With this work, the artist transforms an everyday object into a work of art by labeling and recontextualizing it. DuChamp’s later thought- experiment, the Inframince, is an example of an actively reconstructed piece. In it, viewers contemplate the least-measurable quantities of human expression and perception – the warmth of a seat which has just been left, or the last people hurrying through the closing doors of a subway [1]. These works exist first in written or aural form – the medium is human language. The language is executed in the minds of the readers and listeners, creating a tactile, rich artwork experienced and substantially created in the viewers mind.
Alan Turing's Universal Computer bears a strong resemblance to the rule-based improvisation of jazz and conceptual art, as it fuses instructions and execution in the dynamic process of creation. The Universal Computer is itself a purely conceptual work, since, strictly, is it impossible to build such a machine. It consists of a set of three instructions, which are executed by a computer reading a single, infinitely long paper tape. The tape may either advance by one instruction, rewind by one instruction, or write a symbol at the current spot on the tape In other words, the instructions on the tape tell the computer how to modify both the tape itself and the computer’s internal state, so that content, process, and the computer itself are constantly changing.
For works involving dynamic computation, the question arises: what is the medium? Is the medium the instructions, the computer, the input/output devices or even the programmer? Or does the realm of computation itself form an abstract creative basis? In the process of creating such an artwork, the artist first translates the concept for a given work into abstract algorithms–conceptualizations of the set of steps necessary to accomplish a computational task. The artist then encodes the algorithms into a set of rules and instructions, which they express in symbolic computer-readable languages such as C or Java. These languages are reliably translated into the specific operating instructions for a given computer by a compiler or interpreter. The computer then uses these instructions like a musician uses improvisational rules to dynamically mediate the input from its sensors with the output of the viewer’s physical environment. Just as different jazz musicians differently interpret the same set of rules, so may different computers, different environments, and different audiences produce uniquely different executions of the rule- based work.
Boundary Functions
Figure 1 Caption: Boundary Functions, 1998. Courtesy of Tokyo Intercommunications Center.
As an example of this type of computational improvisation, consider Boundary Functions (1998) (Figure 1). Boundary Functions uses an artifact of computation to create meaning outside the system of computation itself. Through the work, viewers are made to realize that they only have personal space when other people are around them, and that, more generally, reality is a mutual, rather than individual, construction. The work creates a dynamic diagram around the viewers standing on a large platform. The diagram delineates the personal space of each viewer–that is, the space that is closer to any one viewer than to any other. The resulting diagram changes as viewers move on, join, or leave the platform. Structures analogous to these diagrams occur spontaneously throughout nature, such as in the formation of bubbles, the influence of stars on matter (Figure 2), the settlement patterns of animals and the cells of our own bodies. The patterns are referred to as Voronoi diagrams, after the Ukranian mathematician who precisely defined their construction.
Figure 2: Caption: The first know depiction of a Voronoi diagram by Descartes, 1644, showing the gravitational influence of stars.
To produce its result, Boundary Functions uses an algorithmic chain of cause-and-effect. Above the floor, a camera is connected to a computer, which is in turn connected to a projector. First, the camera captures an image of the people standing on the platform. Next, a morphological algorithm is applied to the image to get rid of small variations, and fill the holes in the noisy image of the people below. After that, the instructions specify how to trace the contour of each continuous shape in the image, and then how to find each region’s center. This process reduces the hundreds of thousands of pixels in the image to a few points, each of which represents the location of one person below. The process is one of abstraction and meaning making. Although there is now a hundred thousand times less information than there was in the original image, this information can be used to construct greater meaning in the minds of the viewers.
These points on the simplified image then become the input to the next computational step – the creation of the Voronoi diagram. A particular class of algorithm called “divide- and-conquer” produces this diagram by subdividing all the points until the computer code is only examining two points at a time. The algorithm computes the line that separates these two points, and then moves on to two other points. When all the pairs have been divided by lines, the algorithm merges the lines that are side-by-side, until the entire diagram is constructed.
The resulting Voronoi diagram is then drawn into a memory buffer, using a technique called rasterization that translate from the geometric description of the lines into the pixels within the computer’s memory. Finally, the digital projector converts the memory pixels into light, and then projects the entire image back onto the floor below.
The bulk of the expression of Boundary Functions is through computational processes. Computation provides the means to translate the concept of the algorithm into a perceptual event, creating a dynamic, physical experience for the viewers. Secondary to these aspects, are the ancillary mechanical and physical aspects of the work. In this case, these are the reliable operation of camera, computer and projector, the construction of the floor and lighting of the space. The medium of the artwork is predominantly in the engineering of the dynamic reactive experience through principles of computation.
It’s Out
It’s Out (2001), represents a less physical approach to interactivity. The work consists of a screen-based interactive environment that exists on a web page. The work is inspired by a Chinese koan, succinctly described by Huston Smith in The World’s Religions [2]:
Li-Ku, a high ranking officer in the Tang dynasty, asked a famous Chan master: "A long time ago a man kept a goose in a bottle. It grew larger and larger until it could not get out of the bottle any more. He did not want to break the bottle, nor did he wish to harm the goose. How would you get it out?"
The master was silent for a few moments, then shouted, "Oh officer!" "Yes."
"It's out."
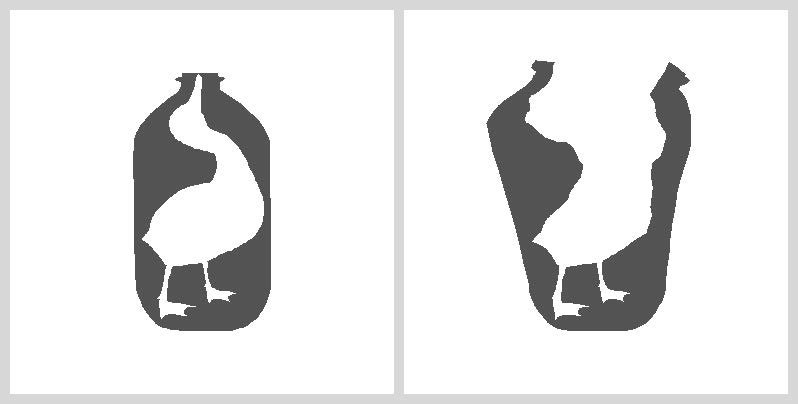
Figure 3 Caption: It’s Out. 2001. Courtesy the Artist.
In attempting to create an interactive representation of the koan in this story, I sought to portray the non-duality hinted at by the koan itself. In general, a koan is not answerable, but through contemplating the question, the meditator may clear away his own misunderstandings through a realization of the non-duality of all things and, ultimately, obtain enlightenment. To re-present this koan visually, I sought to create an illusion of duality that is shattered through interaction with the viewer.
The work begins with a representation of a white goose almost wholly contained in a black bottle (Figure 3). Viewers interact with the work by moving a mouse with their hand. When the viewer clicks and drags within the bottle, the bottle and the goose are revealed to exist only as the contours of a single black object–the outer contour is the bottle and the inner, the goose. This bottle-goose object distorts like soft rubber as the viewer manipulates its surface. The goose and the bottle are no longer distinguishable, nor is it possible to reconstruct their dual existence.
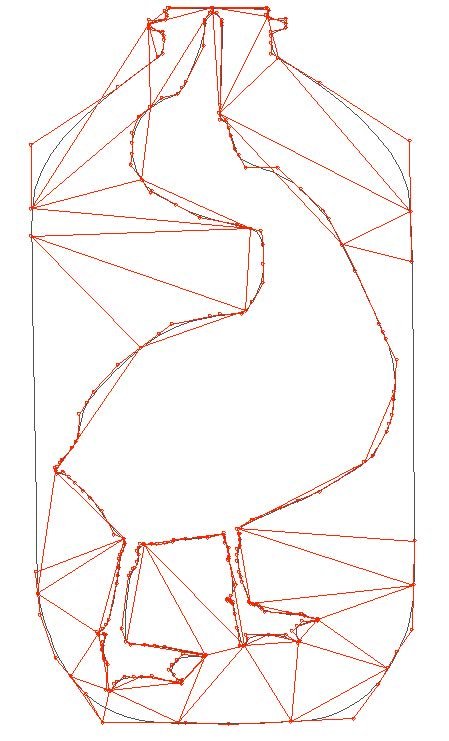
Figure 4 Caption: Springs and masses used to simulate a goose in a bottle. Courtesy the Artist.
For this work, I relied on techniques from the simulation domain of computation. Simulations are used to create virtual representations of bridges, airplanes and buildings and to test their structural properties before they are built. Such simulations function by reducing the vast number of particles composing an object into a simpler set of larger, “finite elements”, to which Newtonian physical principles can be applied. It’s Out is created using such a simulation. I originally drew the starting image in Photoshop, then carefully traced its outline with a single Bezier curve. Bezier curves are mathematically defined to create a smoothly changing contour from a small number of points. The numbers corresponding to these coordinates are included as the starting information for the program. These points are then interpreted as the positions of simulated masses. Between the masses are attach virtual springs which hold the structure together (Figure 4). Every thirtieth of a second, the program computes all of the forces on the masses caused by the springs. It then integrates these forces to calculate first the velocity and then the position of each mass for the current time. Then, the contour points are used to draw a new Bezier curve on the screen. When viewers drag their mouse, the dragging causes a force-field to emanate from the point on the screen, pushing the points of the contour with greater or smaller force depending on distance.
Each time someone runs the program, the work is different, but the overall quality is the same – that of simultaneous unification and disintegration of the form. In this process, some viewers also see a sense of the principle of entropy – the movement of all natural things towards disorder – just as some view Humpty-Dumpty as representing entropy in Lewis Carol’s Alice In Wonderland.
Where is the work?
A detailed exploration of these two works reveals that their nature is essentially computational. Interactive artwork creates a system reactive to the viewer. In the case of these two pieces, the work cannot be even partially experienced without interaction.
Thus, the primary medium of the work is the means for creating this interactivity. This is neither the sensor, nor the computer, code, or output device, but the intangible in- between. Computation provides the substance in which algorithmic and reactive principles can be embodied in a physical computer and connected to the world and to the human viewers of the works. The ultimate construction of meaning in these works occurs in this computational domain.
de Duve, Thierry. Pictorial Nominalism: On Marcel Duchamp’s Passage from Painting to the Readymade. 1984. Trans. Dana Polan and Marjorie Perloff. Minneapolis: Minnesota. 1991.
Smith, Huston. The World’s Religions. New York: Harper Collins. 1992.